Электропривод, как устройство, широко применяется в разных прикладных и научных областях. Чаще всего это электромашиностроение, радиоэлектроника, автомобилестроение, автоматика и вычислительная техника. Для моделирования работы электроприводов при меняются многоконтурные схемы. Оптимальным и эффективным способом является математическое моделирование двухконтурной системы электропривода, и с подобными задачами создания цифровых моделей успешно справляется ПО REPEAT — модельно-ориентированная среда проектирования и математического моделирования. В данной статье описан процесс разработки двухконтурной системы электропривода постоянного тока. По заданным параметрам производится выбор подходящего электродвигателя постоянного тока. С использованием ПО REPEAT создаётся динамическая модель электропривода на основе передаточных характеристик электродвигателя, блока питания (БП), датчиков тока (ДТ) и тахогенератора (ТГ) и проводится синтез регулятора тока и скорости. Модель исследуется с помощью анализа переходных процессов и сравнения с расчетными значениями.

Вводная информация для создания модели

Функциональная схема следящего электропривода

Структурная схема электропривода состоит из потенциометра, усилителя, электродвигателя постоянного тока (ЭД ДПТ), редуктора и тахогенератора (см. Рисунок 1).

Потенциометр является элементом задающего. Управляющие сигналы с выхода потенциометра подаются на вход усилителя, нагрузкой которого является обмотка якоря ЭД постоянного тока с независимым возбуждением.

ЭД через редуктор поворачивают механизм с угловой скоростью, пропорциональной задающему воздействию.

Рисунок 1. Структурная схема следящего электропривода

Тахогенератор образует жесткую обратную отрицательную связь (ООС) по угловой скорости и обеспечивает формирование на входе усилителя сигнала отклонения угловой скорости поворота нагрузки от заданных значений.

В этой статье представлена система замкнутого электропривода (ЭП), построенного по принципу подчиненного регулирования координат на базе REPEAT. Система многоконтурная, она состоит из контура скорости и тока. Каждый контур такой системы настраивается отдельно.

Расчет мощности и выбор электродвигателя постоянного тока

Исходя из требуемых параметров, указанных ниже, проводятся расчеты по выбору ЭД ДПТ и его динамической модели:

- требуемая угловая скорость нагрузки

- требуемое угловое ускорение нагрузки

- момент инерции нагрузки

- статический момент сопротивления нагрузки ;

- КПД редуктора .

1. Для начала необходимо перевести угловую скорость поворота нагрузки из единиц измерений «с» в «рад/с» и угловое ускорение поворота нагрузки из «град/с²» в «рад/с²»:

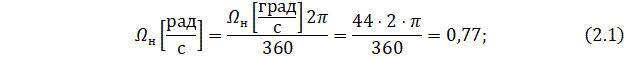
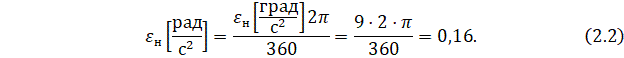
Рассчитывается требуемая мощность:

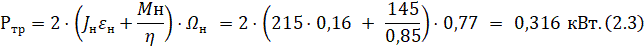
2. Выбирается ЭД, номинальная мощность на валу, которого больше требуемой ( ˃ ).

Относительно вычисленных параметров выбирается электродвигатель МИ-22Ф. Данный двигатель является реверсивным исполнительным двигателем постоянного тока параллельного возбуждения. Предназначен для работы в схемах автоматического управления. Технические данные приведены в Таблице 1.

Таблица 1. Технические данные ЭД МИ-22Ф

3. Рассчитывается оптимальное передаточное число редуктора , согласно формуле:

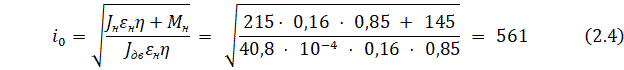
4. Проверяется выбранный ЭД на соответствие требований по скорости.

Следующей формулой определяется номинальная угловая скорость :

и приведенная к валу ЭД угловая скорость поворота нагрузки:

Так как , то требования по скорости не выполняются.

Рассчитывается новое передаточное число редуктора по формуле:

5. Рассчитывается значение требуемого вращающего момента двигателя:

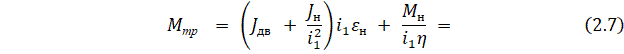
6. Проверяется выбранный ЭД на соответствие требований по моменту:

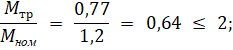
Требования по моменту выполняются.

7. Вычисляются параметры динамической модели ЭД.

7.1. Определяется коэффициент противо-ЭДС:

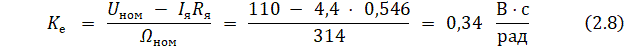
7.2. Определяется коэффициент момента:

7.3. Определяется электромеханическая постоянная времени ЭД:

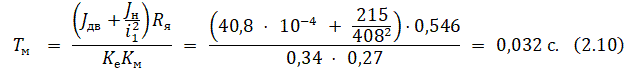
7.4. Для определения электромагнитной постоянной времени ЭД вычисляется индуктивность якоря:

Принимается L_я = 0,0022 Г.

Вычисляются параметры и коэффициенты электродвигателя:

Электромеханический коэффициент:

Коэффициент момента двигателя:

Электромагнитный коэффициент:

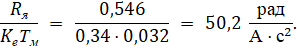
С учетом полученных численных значений структурной схемы динамической модели, ССДМ ЭД принимает следующий вид (см. Рисунок 2):

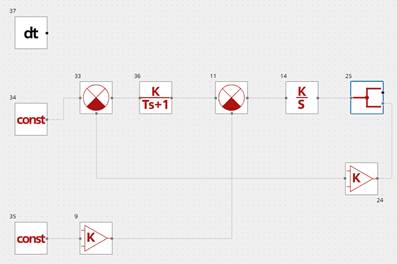
Рисунок 2. Структурная схема динамической модели электродвигателя с числовыми значениями

Переходные характеристики

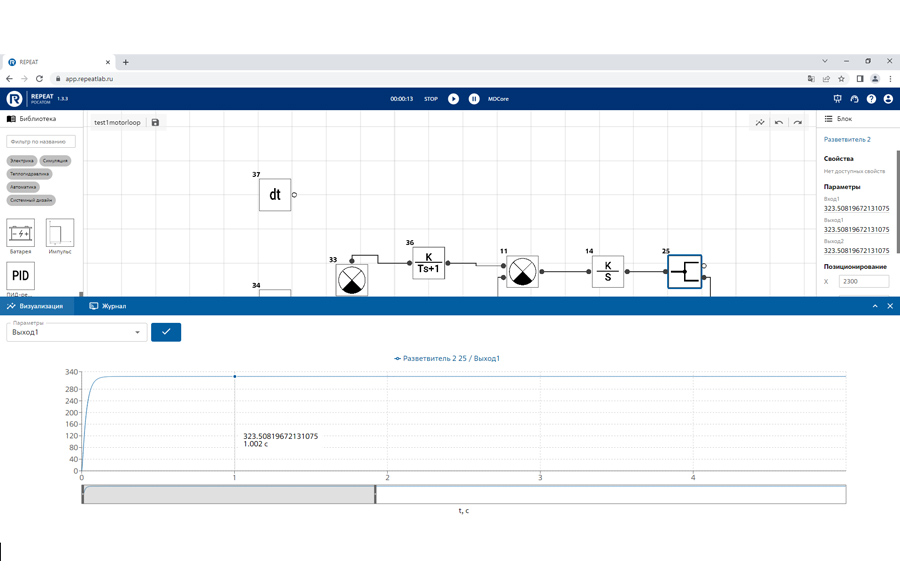
Ниже представлены результаты моделирования при следующих входных параметрах ЭД серии МИ-22 (см. Рисунок 3 и Рисунок 4).

- напряжение питания U_ном = 110 В;

- номинальный момент M_ном = 1,2 ;

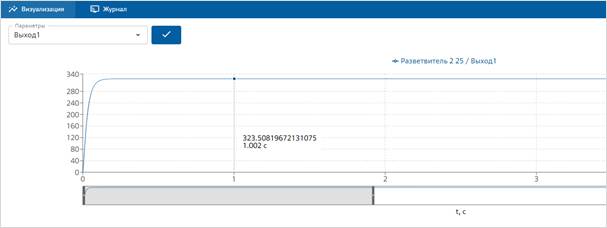
Рисунок 3. Переходная характеристика двигателя ЭД серии МИ-22 по задающему воздействию

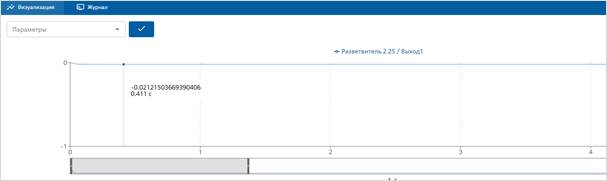
Рисунок 4. Переходная характеристика двигателя ЭД серии МИ-22 по возмущающему воздействию

Анализ переходный характеристик

Определяется относительная погрешность по формуле:

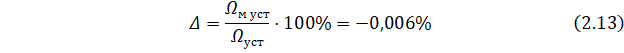
Паспортное номинальное значение угловой скорости вращения ЭД МИ-22 составляет и незначительно отличается от результатов моделирования (323.5 рад/с). Это позволяет сделать вывод о правильности проведённых расчётов.

Настройка контура тока

Динамические свойства БП с большой степенью точности описываются инерционным звеном с передаточной функцией :

Динамические свойства ДТ также описываются инерционным звеном

Теперь можно представить динамическую модель контура тока на базе ПО REPEAT (см. Рисунок 5).

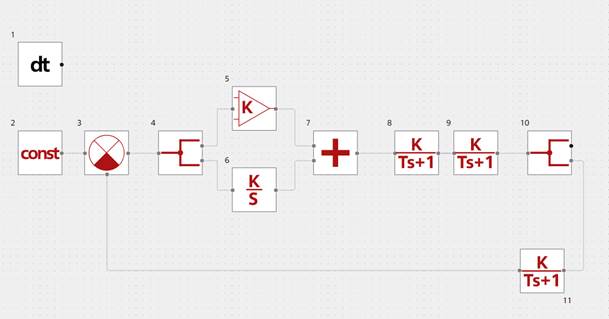
Рисунок 5. Структурная схема динамической модели контура тока

В соответствии со структурной схемой динамической модели контура тока находится передаточная функция разомкнутого контура тока:

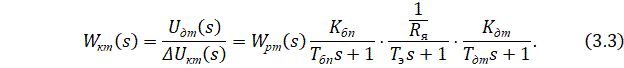
Контур тока (КТ) настроим на оптимум по модулю (ОМ). Передаточная функция КТ, настроенного на ОМ:

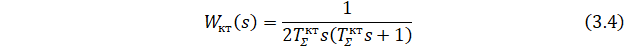
где - суммарная малая постоянная времени КТ. Для ее вычисления определяется постоянная времени БП :

Тогда

Для нахождения передаточной функции регулятора тока (РТ) необходимо приравнять правые части выражений (3.3) и (3.4):

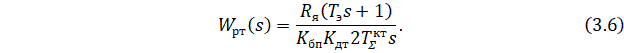
Полученное выражение по своей структуре является передаточной функцией ПИ-регулятора:

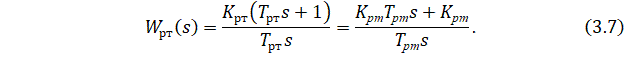
Из сравнения двух последних формул, можно получить формулы для расчета коэффициента передачи K_рт и постоянной времени Т_рт РТ:

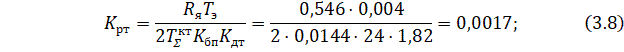
Для вычисления коэффициента передачи датчика тока необходимо применить формулу:

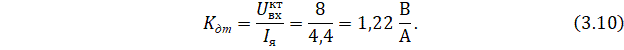
Для построения контура тока в соответствии с (3.6) вычисляется передаточная функция регулятора тока:

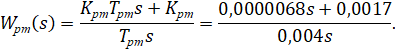
Переходная характеристика

Преамбула с указанием (см. Рисунок 6).

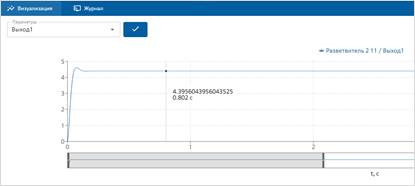
Рисунок 6. Переходная характеристика контура тока по задающему воздействию (значение задающего воздействия на КТ равно 8 В)

Анализ переходной характеристики

Определяется величина перерегулирования σ_кт и время нарастания .

Перерегулирование рассчитается по формуле:

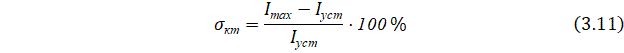
Ожидаемое значение перерегулирования при настройке на ОМ

По рис. 7 определяется максимальное отклонение тока якоря:

и установившееся значение тока:

Определяется перерегулирование:

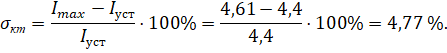
Значение перерегулирования соответствует правильной настройке.

Время нарастания определяется в первой точке пересечения графика переходной функции и установившегося значения тока якоря:

.

Из графика (рис. 6) находится время нарастания :

Время нарастания можно рассчитать, и оно должно удовлетворять требованию:

.

Отклонение измеренного и рассчитанного значения :

Отклонение небольшое и допустимое. Можно сделать вывод, что настройка контура тока на оптимум по модулю проведена успешно.

Настройка контура скорости на симметричный оптимум

Контур скорости (КС) состоит из следующих элементов:

- регулятора скорости (РС) F1;

- КТ, настроенного на ОМ;

- электромеханической части двигателя;

- тахогенератора (ТГ).

Перед тем как приступить к построению схемы КС, необходимо представить все элементы контура в виде звеньев.

Динамические свойства ТГ (инерционное звено):

Настройка контура скорости проводится на симметричный оптимум (СО).

При настройке КС на СО выражение в зоне рабочих частот из-за малости значений постоянных времени T_дт и передаточная функция контура тока может быть представлено в упрощенном виде:

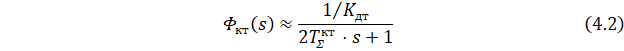
Передаточная функция разомкнутого КС :

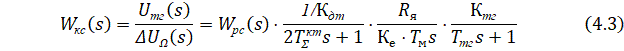
где – суммарная малая постоянная времени КС.

Передаточная функция КС , настроенного на СО, имеет вид:

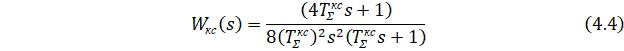
Для определения структуры РС необходимо приравнять правые части выражений (4.3) и (4.4):

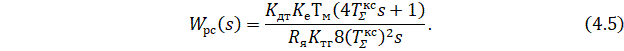
Введем обозначения для получения формулы ПИ-регулятора:

Коэффициент передачи РС :

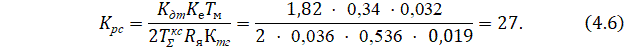
Постоянная времени РС:

Тогда передаточная функция регулятора скорости контура примет вид:

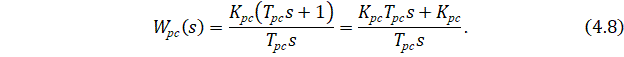
Вычисляется требуемый коэффициент передачи ТГ по формуле:

Передаточная функция регулятора скорости по формуле (4.8):

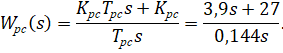
Рассчитывается коэффициент передачи редуктора

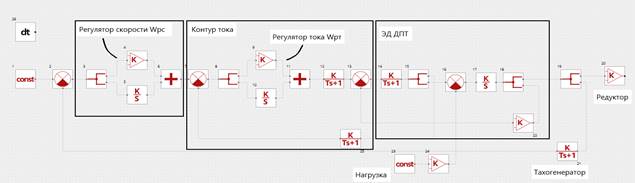
Рисунок 7. Структурная схема динамической модели контура скорости

Переходные характеристики

Построим выходные характеристики и проведем анализ полученных результатов.

1. Построение переходной характеристики КС по задающему воздействию. Значение задающего воздействия на КС = 6 В.

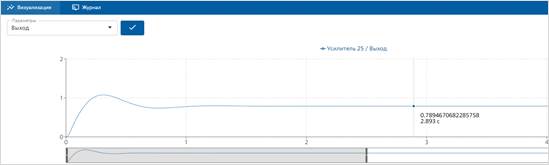
Рисунок 8. Переходная характеристика контура скорости по задающему воздействию

2. Построение переходной характеристики КС по возмущающему воздействию (статическому моменту сопротивления нагрузки). Нагрузка М_н = 145 Н ∙ м.

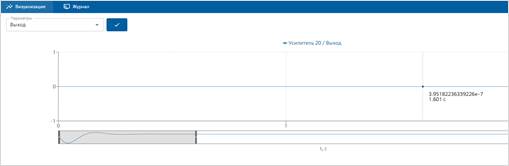
Рисунок 9. Переходная характеристика контура скорости по возмущающему воздействию

Моментная составляющая ошибки в установившемся режиме сводится к нулю.

Анализ переходных характеристик

Максимальное отклонение угловой скорости вращения вала ЭД и установившееся значение

Ожидаемое значение перерегулирования при настройке на СО

Перерегулирование σ_кс:

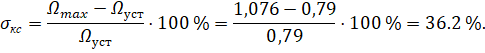
Отклонение от ожидаемого значения составляет и принимается допустимым.

Время нарастания полученной характеристики :

Расчетное значение :

Отклонение измеренного и рассчитанного значения :

Отклонение по допустимое. Настройка контура скорости на оптимум по модулю проведена успешно.

Результаты моделирования

В данной статье была разработана динамическая модель следящего электропривода постоянного тока и проведен синтез регулятора тока и скорости (двухконтурной системы) с применением методов стандартных настроек таких как оптимум по модулю и симметричный оптимум. В ходе работы был выбран электродвигатель постоянного тока МИ-22Ф.

Для задачи создания цифровой модели было успешно использовано ПО REPEAT. Результаты моделирования и расчетные значения показали, что контур скорости и тока был настроен верно с допустимыми значениями отклонений.